점추정과 구간추정
A. 통계적 추론 - 추정 개요
1. 추정 개념
- 모수의 추정에 사용되는 두 가지 방법의 의미와 중요성에 대해 논의합니다.
- 표본을 통해 모집단의 모수를 추정하는 것은 통계학의 중요한 분야 중 하나입니다.
- 모수는 모집단의 특성을 보여주는 값으로, 일반적으로 \( \theta \) (세타)로 표현한다.
2. 점추정과 구간추정
- 점추정 (Point Estimation): 하나의 모수를 하나의 값으로 추정합니다. 이는 표본 데이터를 바탕으로 한 모집단의 모수 추정치를 제공합니다.
- 구간추정 (Interval Estimation): 모수가 포함될 가능성이 있는 구간으로 모수를 추정합니다. 이는 신뢰도를 기반으로 한 범위 안에서 모수가 존재할 확률을 제시합니다.
• 점추정 (Point Estimation)
점추정은 모집단의 모수(예: 평균, 비율)를 하나의 수치로 추정하는 방법입니다.
예시:
전체 중 100명의 학생들의 수학 시험 점수 평균을 살펴보았을 때, 그 평균이 75점이라고 할 때,
이 75점이 바로 점추정값이 됩니다. 이것은 우리가 관심 있는 모집단 전체의 평균 점수를 대표하는 한 점의 추정치입니다.
• 구간추정 (Interval Estimation)
구간추정은 모수가 있을 것으로 예상되는 값의 범위를 제공합니다. 이 범위는 주로 신뢰구간을 통해 표현되며, 우리는 이 구간 안에 모수가 존재할 것이라고 '신뢰'할 수 있습니다.
예시:
위와 같은 상황에서 95% 신뢰 구간을 구했을 때, 그 구간이 72점에서 78점이라면, 모평균은 이 범위 안에 있을 확률이 95%라고 할 수 있습니다.
B . 신뢰구간 (Confidence Interval)
모수 \( \theta \)에 대한 신뢰구간 도출을 위해서는 다음을 알아야함
- 추정량 \( \hat{\theta} \)
- 추정량 \( \hat{\theta} \)의 표본분포 : 일반적으로 모수 \( \theta \)에 의존함
- 모평균 \( \mu \)에 관한 신뢰구간(신뢰수준 : 1 - α)
- 모수 : 모평균 \( \mu \) ▷ ▷ ▷ ▷ \( \theta \)
- 추정량 : 표본평균 \( \bar{X} \) ▷ ▷ ▷ ▷ \( \hat{\theta} \)
- 신뢰수준 확률 : (1-α)
- 오차율 : α
1. 추정량의 표본분포
- \(X_1, X_2, \ldots, X_n\) 이 모평균 \( \mu \) 과 모분산 \( \sigma^2 \) 이 알려진 정규분포 \( N(\mu, \sigma^2) \) 에서의 확률표본이 경우,
\[ \bar{X} \sim N\left( \mu, \frac{\sigma^2}{n} \right) \]
- 이는 \( Z \) 변환을 통해
\[ Z = \frac{\bar{X} - \mu}{\frac{\sigma}{\sqrt{n}}} \sim N(0, 1) \]
* 참조: 보통 모분산 \( \sigma^2 \) 이 현실적으로는 알려진 경우가 없다. > 과거 경험으로 알려줬거나 이론적으로 이렇게 해야한다는 것이 없으면 보통 추정해야한다.
중심극한정리에 의하면 표본평균은 근사적으로 정규분포를 따르고 표준화된 Z는 표준정규분포를 따른다.

\[ P(-z_{\alpha/2} \leq Z \leq z_{\alpha/2}) = 1 - \alpha \]
\[ P\left(-z_{\alpha/2} \leq \frac{\bar{X} - \mu}{\sigma/\sqrt{n}} \leq z_{\alpha/2}\right) = 1 - \alpha \]
\[ P\left(\bar{X} - z_{\alpha/2} \frac{\sigma}{\sqrt{n}} \leq \mu \leq \bar{X} + z_{\alpha/2} \frac{\sigma}{\sqrt{n}}\right) = 1 - \alpha \]

2. 신뢰구간의 해석
신뢰수준은 동일한 구간추정법을 반복적으로 사용할 떄 얻어지는 신뢰구간들이 참값 \(\theta \)를 품을 확률을 의미한다.
단, n 개의 표본으로 구한 하나의 신뢰구간에 모수가 포함되었는지 여부는 알 수 없다
즉, 모수가 포함될 수 있는 가능성이 높도록 디자인이 되어있을 뿐이지 포함 여부는 알 수 없다.
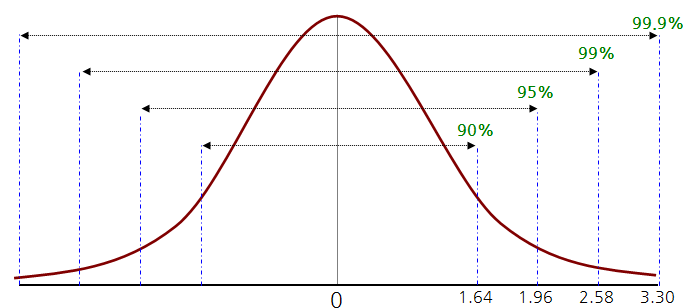
| 신뢰수준 | 유의수준 양쪽 | Z값 찾기 | Z값 | 임계값찾기 |
|---|---|---|---|---|
| 90% | 10.0% (양쪽) | 1 - 0.5 - 0.100 | 0.4000 | 1.2870 |
| 5.0% (양쪽) | 1 - 0.5 - 0.050 | 0.4500 | 1.6450 | |
| 95% | 5.0% (양쪽) | 1 - 0.5 - 0.050 | 0.4500 | 1.6450 |
| 2.5% (양쪽) | 1 - 0.5 - 0.025 | 0.4750 | 1.9600 | |
| 99% | 1.0% (양쪽) | 1 - 0.5 - 0.010 | 0.4900 | 2.3250 |
| 0.5% (양쪽) | 1 - 0.5 - 0.005 | 0.4950 | 2.5750 |
예제1
90% 신뢰수준에서 모평균의 신뢰구간을 구해봅시다. 표본 평균이 50, 표본 표준편차가 10이고, 표본 크기가 30입니다. 90% 신뢰수준에서 Z값은 약 1.645입니다.
표본 평균: 50
표본 표준편차: 10
표본 크기: 30
Z값(90%): 1.645
신뢰구간: 50 ± (1.645 * 10 / √30)
신뢰구간: 50 ± 3.00
따라서, 신뢰구간은 대략 47에서 53 사이입니다.
예제2
어떤 상점에서 판매하는 생선의 체장을 파악하고자 7마리를 추출하여 그 체장을 조사하였더니 다음과 같았다.
생선의 체장은 정규분포를 따르며, 고등어 체장의 표준편차가 1.5로 알려져 있다고 할때 (90%신뢰 수준에서) 생선 체장의 신뢰 구간을 구해보자
28.9, 32.9, 29.8, 30.6, 27.8, 29.4, 31.3
표본 평균 \( \bar{X} \) : 30.029
표본 표준편차 \( \sigma \) : 1.5
표본 크기 n: 7
Z값(90%): 100(1-0.10)% : z_{\0.10/2} \) = 1.645
신뢰구간:
\( \bar{X} \) ± z_{\alpha/2} \frac{\sigma}{\sqrt{n}}\)
30.029 ± (1.645 * 1.5 / √70)
= 29.096, 30.962
(29.096, 30.962)에 모평균이 포함되며 이를 90% 신뢰할 수 있다.
중요한 점
구간이 모수를 항상 포함하도록 만들어진 것은 아닙니다. 대신, 장기적으로 보았을 때 해당 구간이 모수를 포함할 확률이 신뢰수준(예: 95%)만큼 되도록 계산됩니다. 즉, 같은 방식으로 100번의 추정을 했을 때, 약 95번의 신뢰구간이 실제 모수를 포함할 것으로 기대할 수 있습니다.
'기초 통계' 카테고리의 다른 글
| No12.가설검증의 원리 (1) | 2024.04.22 |
|---|---|
| No10.[추정과 검정]통계적 추론 개요, 표본추출법 (1) | 2024.04.17 |
| No09_그래프에 의한 기술통계 (0) | 2024.04.16 |
| No08_수치적 기술통계 - 연관성 (1) | 2024.04.14 |
| No07_수치적 기술통계 - 변동성 (1) | 2024.04.13 |



