[탐색적 데이터 분석]
A. 중심 위치 척도
탐색적 데이터 분석에서 중심위치척도는 데이터 집합의 대표값을 의미합니다. 이를 통해 데이터가 어느 지점에 위치하는지를 파악할 수 있죠. 대표적인 중심위치척도에는 평균(mean), 중앙값(median), 최빈값(mode)이 있습니다.
- 평균(Mean)은 모든 데이터 값의 합을 데이터의 개수로 나눈 값입니다. 데이터의 총합을 대표하는 가장 일반적인 척도
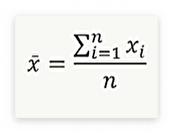
- 중위수, 중앙값(Median)은 데이터를 크기 순으로 나열했을 때 중앙에 위치하는 값입니다. 이상치의 영향을 덜 받아서 때때로 평균보다 선호되기도 해요.

- 최빈값(Mode)은 데이터 집합에서 가장 자주 나타나는 값입니다. 범주형 데이터에서 유용하게 사용되죠.
이 세 가지 척도를 함께 분석하면 데이터의 분포와 형태에 대해 좀 더 풍부한 이해를 얻을 수 있습니다. 데이터의 전반적인 경향을 파악하는 데 있어서 중요한 단계이며, 복잡한 데이터 집합에서 중요한 인사이트를 도출하는 데 기초가 되는 지표입니다.
※ 분포의 치우침 유형 별 중심위치 척도들 간의 관계
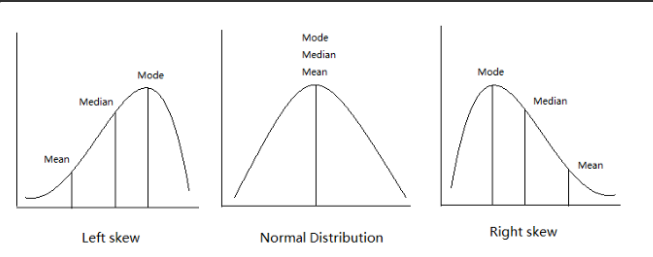
B. 상대적 위치 척도
상대적 위치척도는 데이터 내 특정 값이 전체 데이터 분포에서 어느 위치에 있는지를 상대적으로 나타내는 척도입니다. 주요 상대적 위치척도에는 사분위수(Quartiles), 백분위수(Percentiles), 그리고 표준점수(Z-scores)가 있습니다.
- 사분위수는 데이터를 네 등분한 값으로, 중앙값을 포함해 일반적으로 Q1(25번째 백분위수), Q2(중앙값 혹은 50번째 백분위수), Q3(75번째 백분위수)로 표현됩니다.

- 백분위수는 데이터를 백 등분한 값으로, 예를 들어 90번째 백분위수는 전체 데이터 중 90%가 이 값 이하에 위치함을 나타냅니다. 예를 들어, 성적이 상위 20%에 속한다면 그 성적은 80번째 백분위수에 해당합니다. 이는 그 성적이 전체의 80%보다 같거나 높고, 상위 20% 이내에 있다는 것을 의미합니다.
- 표준점수(Z-score)는 개별 데이터가 평균으로부터 얼마나 멀리 떨어져 있는지를 표준편차의 배수로 나타내는 값입니다. 데이터가 평균에서 몇 표준편차만큼 떨어져 있는지를 나타내는 척도로, 공식은 (관측값 - 평균) / 표준편차입니다. 예를 들어, 평균이 100이고 표준편차가 15인 시험에서 130점을 받았다면, Z-점수는 (130 - 100) / 15 = 2가 됩니다. 이는 해당 점수가 평균보다 2표준편차 위에 있다는 것을 의미하며, 이 점수가 얼마나 특출한지를 나타냅니다.
이러한 척도들은 데이터의 위치와 분포를 이해하는 데 매우 중요하며, 특히 이상치 탐지나 다른 데이터 집합과의 비교에 유용하게 사용됩니다.
C.변동성 척도
변동성 척도는 데이터의 퍼짐 정도, 즉 데이터가 얼마나 변동하는지를 나타내는 통계적 수치입니다. 대표적인 변동성 척도에는 범위(range), 사분위간 범위(interquartile range, IQR), 분산(variance), 표준편차(standard deviation) 등이 있습니다.
- 범위는 데이터의 최댓값과 최솟값의 차이입니다. 간단하면서도 직관적인 변동성의 척도이지만, 이상치에 매우 민감합니다.
- 사분위간 범위(IQR)는 제3사분위수(Q3)와 제1사분위수(Q1)의 차이로, 중간 50% 데이터의 퍼짐 정도를 나타냅니다. 이상치의 영향을 덜 받는다는 장점이 있습니다.
- 분산은 각 데이터 값과 평균의 차이를 제곱한 뒤 평균을 낸 값으로, 데이터가 평균으로부터 얼마나 떨어져 있는지를 나타내는 척도입니다.
- 표준편차는 분산의 제곱근으로, 분산과 마찬가지로 평균에서의 퍼짐 정도를 나타내지만, 단위가 원래 데이터와 같아 해석하기 쉽습니다.

★ 표본분산에서 n-1로 나누는 이유는 '불편추정량(unbiased estimator)'에 기인합니다.
이는 표본에서 계산한 분산이 모분산을 더 정확히 추정할 수 있게 해주는 방법입니다.
간단히 말해, 표본의 크기인 n으로 나누면 표본분산이 모분산보다 적게 추정되는 경향이 있는데,
이를 보정하기 위해 n-1로 나누는 것입니다. 이는 표본의 자유도를 고려한 것으로,
표본의 평균이 하나의 추정값으로 사용됨으로써 한 개의 자유도를 잃기 때문입니다.
변동성 척도는 데이터의 일관성, 안정성 및 예측 가능성을 이해하는 데 중요한 도구로 사용됩니다. 예를 들어, 두 주식의 표준편차를 비교하면 어느 주식이 더 변동성이 큰지 비교할 수 있습니다.
- 변동계수(CV, Coefficient of Variation)는 표준편차를 평균으로 나눈 값으로, 다른 평균을 가진 두 데이터 집합의 변동성을 상대적으로 비교할 수 있게 해줍니다. 변동계수는 특히 평균 값이 크게 다를 때 유용하며, 단위가 없어서 다양한 분야에서 활용됩니다.
[변동계수의 활용]
- 자료의 단위가 다를 경우
- 스케일의 차이가 큰경우
예를 들어, 한 투자자가 두 주식 A와 B를 비교할 때, A의 평균 수익률이 10%이고 표준편차가 2%, B의 평균 수익률이 20%이고 표준편차가 5%라고 가정해 봅시다. 여기서 변동계수를 사용하면, 각 주식의 변동성을 평균 수익률에 대한 상대적 비율로 비교할 수 있으며, 이는 투자의 위험을 평가하는 데 도움이 됩니다.
D.형태 척도
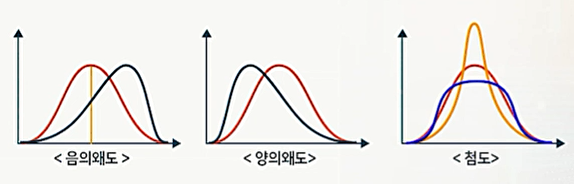
분포의 형태를 나타내는 주요 척도에는 왜도(skewness)와 첨도(kurtosis)가 있습니다.
- 왜도는 데이터 분포의 비대칭성을 측정하며, 양의 왜도는 오른쪽으로 긴 꼬리를, 음의 왜도는 왼쪽으로 긴 꼬리를 가진 분포를 의미합니다.
- 첨도는 데이터 분포의 뾰족한 정도와 꼬리의 두께를 나타내며, 높은 첨도는 더 뾰족한 분포와 두꺼운 꼬리를, 낮은 첨도는 더 평평한 분포와 얇은 꼬리를 의미합니다.
'기초 통계' 카테고리의 다른 글
| No09_그래프에 의한 기술통계 (0) | 2024.04.16 |
|---|---|
| No08_수치적 기술통계 - 연관성 (1) | 2024.04.14 |
| NO.5 정규분포, 표준정규분포 (1) | 2024.04.02 |
| No4.이항분포, 포아송분포, 지수분포, 감마분포 (1) | 2024.03.28 |
| No3.확률변수와 확률분포의 특성치 (0) | 2024.03.28 |



