[탐색적 데이터 분석]
수치적 기술통계에서 연관성을 이해하는 데 중요한 개념에는 공분산, 피어슨 상관계수, 스피어만 상관계수, 켄달의 상관계수가 있습니다. 비선형적 관계나 순위 데이터에 더 적합합니다.
- 공분산은 두 변수 간의 관계의 방향
- 피어슨 상관계수는 두 변수 간의 선형적 관계의 강도와 방향을 측정
- 스피어만 상관계수와 켄달의 상관계수는 순위 기반의 상관 관계를 측정
A. 두 숫자형 변수의 선형적 연관성
- 선형적 연관성의 방향과 강도

1. 양의 연관성
- 하나가 커지면 다른 하나도 커진다.
- 하나가 작아지면 다른 하나도 작아진다
.
2. 음의 연관성
- 하나가 작어지면 다른 하나는 커진다.
- 하나가 커지면 다른 하나는 작아진다.
3. 무상관
B. 연관성의 측도 - 공분산(Covariance)
공분산? 공동 분산 ?
- 분산(Variance): 하나의 변수가 평균으로부터 얼마나 멀리 떨어져 있는지를 나타내는 척도입니다. 분산은 그 변수의 평균값에서 각 데이터 포인트의 차이를 제곱하여 평균낸 값입니다. 분산은 변수 자체의 변동성만을 나타내며, 그 단위는 원래 변수의 단위의 제곱입니다.
- 공분산(Covariance): 두 변수 간의 변동성이 어떻게 함께 움직이는지를 나타내는 척도입니다. 공분산은 한 변수가 그 평균보다 높을 때 다른 변수도 평균보다 높거나 낮은 경향이 있는지를 측정합니다. 공분산의 값이 양수라면 두 변수가 같은 방향으로 변동하고, 음수라면 반대 방향으로 변동합니다. 공분산의 단위는 두 변수의 단위의 곱입니다.
- X의 분산은?
Var(X) = E((X - μₓ)²)
- Y의 분산은?
Var(Y) = E((Y - μᵧ)²)
- X, Y의 공분산은?
COV(X, Y) = E((X - μₓ)(Y - μᵧ))
'X와 Y가 어떠한 방향성을 가지고 있는가' 그것을 보시하는 것입니다.
간단히 말해, 분산은 하나의 변수 내에서의 변동성을 측정하는 반면, 공분산은 두 변수 간의 변동성의 상관 관계를 측정합니다.
표본 공분산 (Sample Covariance)
- n쌍의 표본 자료 \( (x_1, y_1), \ldots, (x_n, y_n) \)이 주어졌을 때,
표본 공분산 \( S_{xy} \)는 다음과 같이 계산됩니다.

- 상관관계의 방향
- \( S_{xy} > 0 \): 양의 상관 관계, 비례관계
- \( S_{xy} < 0 \): 음의 상관 관계, 반비례관계

공분산은 양의 상관이면 크고, 음의 상관이면 작고, 무상관이면 0에 가깝다.
이 '크다'와 '작다'의 의미에 대해서 한번 생각해볼 필요가 있다.
★ 무조건 공분산이 크다고 연관성이 높은가?
- 단위, 범위에 영향을 받는다.
즉, 표준화 시켜줄 필요가 있다.
궁극적인 연관성의 측도 : 상관계수 (Correlation coefiicient)
C. 상관계수 (Correlation coefiicient)
상관계수 (Correlation coefiicient) : 공분산을 표준화하여, 두 변수 간의 선형적 관계의 강도와 방향을 -1에서 1 사이의 값으로 나타냅니다. 이 값이 클수록 변수 간의 선형적 관계가 강하다는 것을 의미합니다.
ex) 실생활 예시: 키와 몸무게, 흡연량과 기대수명
- 키와 몸무게는 일반적으로 양의 상관관계를 보입니다. 키가 클수록 몸무게도 많이 나가는 경향이 있죠.
- 반면, 흡연량과 기대수명은 음의 상관관계를 가지고 있습니다. 흡연량이 많을수록 기대수명은 짧아지는 경향을 보입니다.
모상관계수(ρ)는 모집단의 모든 데이터를 사용해 계산하며, 표본상관계수(r)는 표본 데이터로부터 추정됩니다. 표본상관계수는 '피어슨 상관계수'로도 알려져 있으며, 실제 연구에서 모집단에 대한 전체 정보를 얻기 어렵기 때문에 표본 데이터를 바탕으로 추정하는 것이 일반적입니다.
모상관계수 : X, y의 공분산을 각각의 편차로 나누어 준다.
* ρ (rho라고 읽는다.)
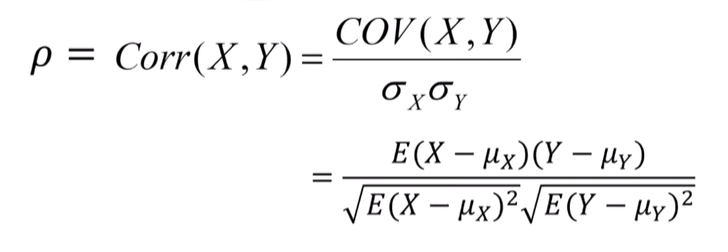
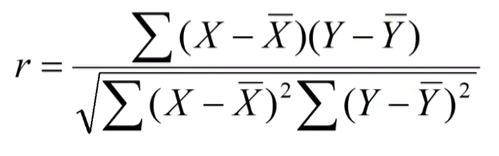
간단한 예제로, 5명의 학생들의 수학 점수와 과학 점수가 다음과 같다고 가정합시다:

1. 먼저, 각 학생들의 수학 점수와 과학 점수의 평균을 계산합니다:
- 수학 점수 평균: (80 + 85 + 78 + 92 + 88) / 5 = 84.6
- 과학 점수 평균: (90 + 95 + 80 + 88 + 85) / 5 = 87.6
2. 각 점수에서 해당 평균을 뺀 후, 이를 서로 곱합니다. 이렇게 계산된 값을 모두 더해줍니다(공분산의 분자 부분):
Σ(xᵢ - x̄)(yᵢ - ȳ) 계산:
(80 - 84.6)(90 - 87.6) + (85 - 84.6)(95 - 87.6) + (78 - 84.6)(80 - 87.6) +
(92 - 84.6)(88 - 87.6) + (88 - 84.6)(85 - 87.6)
= (-4.6)(2.4) + (0.4)(7.4) + (-6.6)(-7.6) + (7.4)(0.4) + (3.4)(-2.6)
= -11.04 + 2.96 + 50.16 + 2.96 - 8.84
= 36.2
3. 각 점수에서 평균을 뺀 값의 제곱의 합을 계산합니다(공분산의 분모 부분):
Σ(xᵢ - x̄)² 계산:
Σ(yᵢ - ȳ)² 계산:
(80 - 84.6)² + (85 - 84.6)² + (78 - 84.6)² + (92 - 84.6)² + (88 - 84.6)²
= 21.16 + 0.16 + 43.56 + 54.76 + 11.56 = 131.2
(90 - 87.6)² + (95 - 87.6)² + (80 - 87.6)² + (88 - 87.6)² + (85 - 87.6)²
= 5.76 + 54.76 + 57.76 + 0.16 + 6.76 = 125.2
4. 마지막으로, 이렇게 계산된 분자를 분모의 제곱근으로 나누어 표본상관계수를 구합니다:
r = Σ(xᵢ - x̄)(yᵢ - ȳ) / √(Σ(xᵢ - x̄)² * Σ(yᵢ - ȳ)²)
r = 36.2 / √(131.2 * 125.2)
= 36.2 / √(16420.24)
= 36.2 / 128.15
= 0.282 (소수점 셋째 자리에서 반올림)
따라서, 학생들의 수학 점수와 과학 점수 사이의 표본상관계수는 약 0.282입니다.
이는 두 점수 사이에 약한 양의 선형 관계가 있음을 나타냅니다.
상관계수의 범위
1. -1에서 1사이의 값 ( -1 <= r <= 1 )
2. r > 0 : 양의 상관관계 / 최대값은 X와 X의 상관계수 = 1
2. r < 0 : 음의 상관관계 / 최소값은 X와 -X의 상관계수 = -1
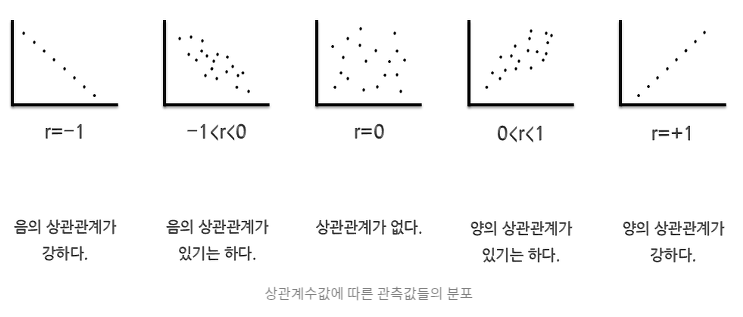
r(상관계수)이 1이나 -1에 가까울수록 x,y의 상관성이 높다고 볼 수 있다.
D.순위를 이용한 상관계수
- 서열 척도이거나, 정규분포를 심하게 벗어나는 두 숫자형 변수의 연관성 파악
스피어만 상관계수(Spearman's rank correlation coefficient)
두 변수의 순위 사이의 통계적 의존성의 강도를 측정하는 비모수적(모집단 분포에 대한 가정이 필요 없는) 방법입니다.
스피어만 상관계수는 피어슨 상관계수와 유사하게 -1부터 +1까지의 값으로 표현됩니다.
이 상관계수는 원본 데이터의 값을 사용하는 대신, 데이터 포인트를 순위로 변환하고 순위에 기반하여 상관관계를 계산합니다. (예 - 오름차순) 이로 인해, 스피어만 상관계수는 원 데이터의 분포가 정규분포를 따르지 않거나, 관계가 선형적이지 않을 때, 또는 이상치의 영향을 받을 때 특히 유용합니다.
간단한 예를 들어, 학생들이 여러 시험을 치뤘을 때 수학과 과학 시험 점수 사이의 스피어만 상관계수를 계산하면, 각 시험에서의 학생들의 성적 순위 간의 상관관계를 알 수 있습니다. 이는 순수한 점수 값이 아닌, 학생들이 어떤 과목에 강한지 혹은 약한지의 경향성을 파악할 때 유용하게 사용됩니다.
E. 상관계수의 한계
1. 상관계수는 만능이 아니다.
2. 수학적 관계이지 속성의 관계는 아니다.
예로 들어 언어 성적과 수학 성적의 상관계수를 구했더니 0.8이 나왔습니다.
굉장히 높은 상관관계를 가졌으니 언어 성적이 높은 사람들은 수학 성적이 높은 것을 확인 했습니다.
다만 여기까지는 맞습니다.
"언어를 잘 하기 위해서는 수학 공부를 열심히 하라", " 수학이 떨어지니 국어 공부부터 열심히 해라" 와 같은 말은 이상ㅏ합니다. 실제로 언어 성적이 높은 사람들이 수학 성적이 높았던 이유는 뭘까요. 공부를 잘하면 둘 다 잘하고 공부를 못하면 둘 다 못하기 때문이었죠. 이렇게 두 변수의 관계는 수학적인 관계이지 속성 간의 관계까지 확장 시키는 것은 매우 위험합니다.
3. 선형관계의 측도이다. - 곡선관계는 찾아내지 못한다.
- 상관계수가 높다고 해서 어떤 변수가 어떤 변수의 원인이 된다라고 이렇게 확대 해석하는 것은 좀 무리라고 할 수 있다.
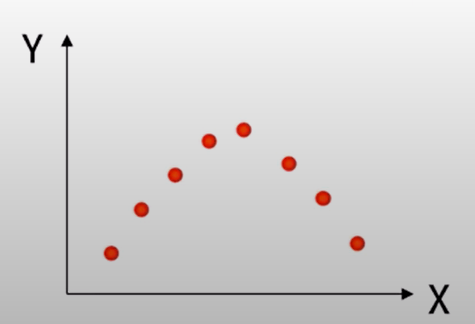
예시 그래프에서 보면 x와 y 간에 관계다. 어떤 관계입니까? x가 증가함에 따라 y도 증가하다가 어느 순간 지나서는 감소합니다. 이것은 선형관계가 아니라 이차함수 관계이죠. 그런데 이것을 가지고 공분산을 구하면 x 평균, y 평균이라 하면 플러스 마이너스가 골고루 분포해서 0이 되어 버립니다.
즉, 상관계수는 곡선 관계를 찾아내지 못하며. 상관관계가 있다는 것은 선형 관계가 있다라는 뜻
4. 자료분석의 초기단계에 이용된다.
상관계수가 높게 나오면 그 다음에 왜 높게 나왔는지를 추후 분석할 필요가 있다
이러한 한계에도 불구하고 매우 간단하고 직관적이라는 이유 때문에 많은 부분에서 사용되고 있습니다.
'기초 통계' 카테고리의 다른 글
| No10.[추정과 검정]통계적 추론 개요, 표본추출법 (1) | 2024.04.17 |
|---|---|
| No09_그래프에 의한 기술통계 (0) | 2024.04.16 |
| No07_수치적 기술통계 - 변동성 (1) | 2024.04.13 |
| NO.5 정규분포, 표준정규분포 (1) | 2024.04.02 |
| No4.이항분포, 포아송분포, 지수분포, 감마분포 (1) | 2024.03.28 |



