통계적 추론은 모집단으로부터 얻은 표본 데이터를 기반으로 모집단의 특성을 추론하는 과정을 말합니다.
이 과정에서는 대부분의 경우, 전체 모집단을 조사하는 것이 불가능하기 때문에, 표본을 통해 모집단에 대한 결론을 내리게 됩니다. 통계적 추론은 크게 추정과 검정의 두 가지 주요 과정으로 나눌 수 있습니다.
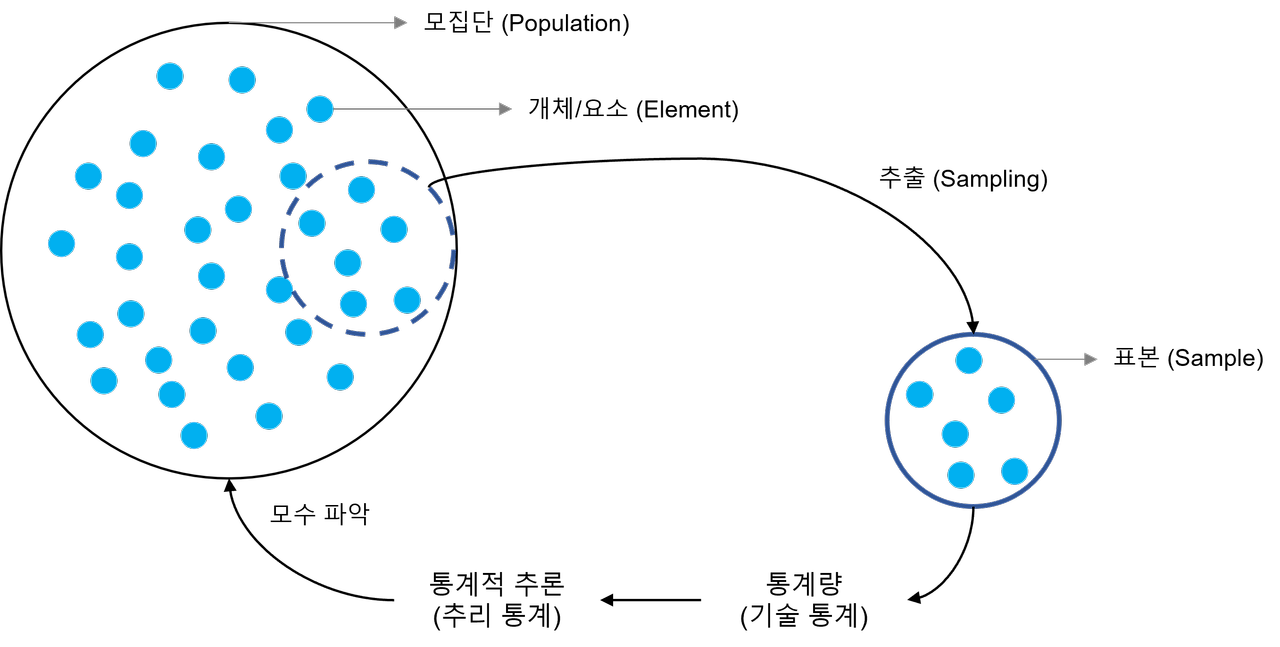
- 모집단(Population): 관심의 대상이 되는 전체 집단으로, 연구나 분석의 대상이 되는 모든 개체나 사건의 집합입니다. 예를 들어, 모든 고등학교 학생, 모든 나무 등이 될 수 있습니다.
- 모수(Parameter): 모집단의 특성을 나타내는 수치로, 예를 들어 모집단의 평균, 분산, 비율 등이 이에 해당합니다. 모수는 일반적으로 알려져 있지 않으며, 통계적 방법을 통해 추정합니다.
- 표본(Sample): 모집단에서 선택된 일부분으로, 모집단의 특성을 추론하기 위해 사용됩니다. 표본은 모집단을 대표할 수 있도록 적절하게 선택되어야 합니다.
- 통계량(Statistic): 표본 데이터를 요약하는 수치로, 표본 평균, 표본 분산 등이 있습니다. 통계량은 모수를 추정하기 위해 사용되며, 표본에 따라 그 값이 달라질 수 있습니다.
- 표본추출(Sampling): 모집단에서 표본을 선택하는 과정입니다. 올바른 표본추출 방법을 사용하는 것은 표본이 모집단을 잘 대표하게 하여, 통계적 추론의 정확성을 높이는 데 중요합니다.
- 통계적 추론(Statistical Inference): 표본 데이터를 기반으로 모집단의 특성에 대해 결론을 내리는 과정입니다. 이 과정에는 추정(모수의 추정)과 검정(가설 검정)이 포함됩니다. 통계적 추론을 통해 모집단에 대한 결론을 유도할 수 있으며, 이는 표본의 정보를 활용하여 불확실성을 관리하는 방법입니다.

A. 통계적 추론 개요
- 추정(Estimation): 추정은 모집단의 매개변수(예: 평균, 분산)를 표본 데이터를 통해 추측하는 과정입니다. 추정에는 점추정과 구간추정이 있습니다. 점추정은 모집단의 매개변수를 하나의 값으로 추정하는 것을 말하고, 구간추정은 주어진 신뢰수준 하에 모집단 매개변수가 포함될 것으로 예상되는 값의 범위를 제시합니다.
- 검정(Hypothesis Testing): 검정은 사전에 설정된 가설(예: 두 집단의 평균은 같다)이 통계적으로 유의한지를 판단하는 과정입니다. 이 과정에서는 귀무가설(Null Hypothesis)과 대립가설(Alternative Hypothesis)을 설정하고, 데이터를 분석하여 귀무가설을 기각할지 여부를 결정합니다.
확률표본 (Probability Sample)
확률표본은 모집단 내의 개체들이 표본에 선택될 확률이 알려져 있고, 각 개체가 무작위로 선택될 수 있는 방법으로 추출된 표본을 말합니다. 이러한 추출 방법을 통해 얻어진 표본은 모집단을 공정하게 대표한다고 볼 수 있으며, 통계적 추론을 할 때 편향 없는 결과를 도출할 가능성이 높아집니다.
통계량 (Statistic)
통계량은 표본 데이터로부터 계산된 값으로, 모집단의 모수(예: 평균, 분산, 비율 등)를 추정하기 위해 사용됩니다. 통계량은 표본에 따라 그 값이 달라지므로, 표본에서 계산된 여러 통계량들은 그 자체로 확률분포를 가집니다.
표본분포 (Sampling Distribution)
표본분포란 특정 통계량의 가능한 모든 값에 대한 확률분포를 말합니다. 예를 들어, 모집단에서 여러 번 표본을 추출하고, 각 표본에 대해 평균을 계산했을 때, 그 평균들은 표본 평균의 분포를 형성합니다. 이 분포를 '표본 평균의 표본분포'라고 부릅니다. 표본분포는 통계량이 어떻게 변동할 수 있는지를 나타내며, 중심극한정리에 따라, 충분히 큰 표본 크기를 가지는 경우 표본 평균의 분포는 정규분포에 근사하게 됩니다. 이러한 표본분포는 통계적 추정과 검정에서 근거로 사용됩니다.
$$
E[\bar{X}] = \mu
$$
$$
\text{Var}(\bar{X}) = \frac{\sigma^2}{n}
$$
\(E[\bar{X}] = \mu\)는 표본 평균의 기대값이 모평균 μ와 같다는 것을 의미합니다. 즉, 여러 표본을 추출하여 평균을 계산하면, 이들 표본 평균의 평균(기대값)은 모집단의 평균에 근접합니다.
\(Var(\bar{X}) = \frac{\sigma^2}{n}\)는 표본 평균의 분산이 모분산 σ^2를 표본의 크기 n으로 나눈 것과 같다는 것을 나타냅니다. 이것은 표본의 크기가 커질수록 표본 평균의 분산이 작아지며, 표본 평균이 모평균 μ에 더 가까워진다는 것을 의미합니다. 이는 중심극한정리의 한 부분으로, 표본의 크기가 크면 클수록, 표본 평균의 분포가 정규분포에 접근한다는 점을 보여줍니다.
B. 표본추출법
표본추출은 모집단에서 일부를 선택하는 과정입니다. 올바른 표본추출 방법을 사용하는 것은 통계적 추론의 정확도를 결정하는 중요한 요소입니다. 주요 표본추출법은 다음과 같습니다.
1. 단순임의추출법 (Simple Random Sampling)
- 모집단을 구성하는 모든 요소에 대해 동일한 확률로 추출될 가능성을 동일하게 하는 추출 방법입니다. 가장 기본적이고, 널리 사용되는 추출 방법입니다.
- 나무에서 나무를 뽑거나 복권에서 복권을 추출하는 것과 같습니다. 예를 들어, N개의 요소로 구성된 모집단에서 n(≤N)개의 표본을 추출할 때 전체 요소에 1, 2, ..., N까지의 번호를 붙여두고 여기서 n개의 번호를 임의로 선택하여 그 번호에 해당하는 요소를 표본으로 추출합니다.
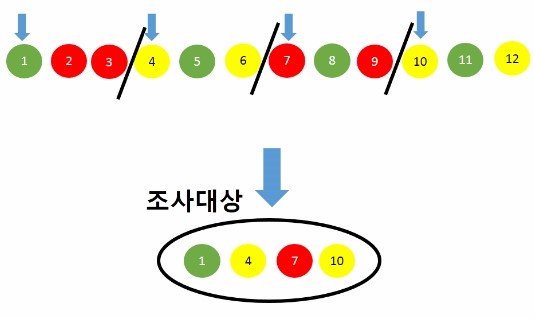
2. 계통추출법 (Systematic Sampling)
- 첫 번째 표본을 랜덤으로 선택한 후, 그 이후의 표본을 일정한 간격으로 선택합니다.(편향의 문제가 발생 할 수 있다.)
- N개의 요소로 구성된 모집단에서 n(≤N)개의 표본을 추출할 때 대상 요소에 1, 2, ..., N까지의 번호를 붙이고 이 중 n개를 나열합니다.
- K(=N/n)번째 n개의 구간으로 나누고, 첫 번째 구간에서 K개의 요소 중 하나를 임의로 선택하여, 그 이후는 K개씩 띄어서 표본을 추출합니다.
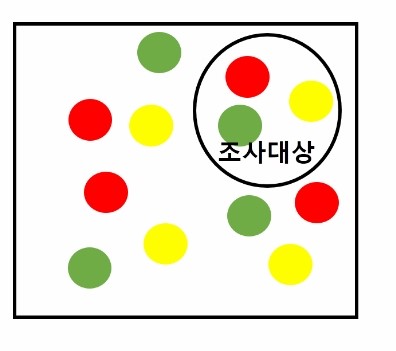
3. 집락추출법 (Cluster Sampling)
- 모집단이 많거나 전달(cluster)이 강력한 형태로 구성되어 있고, 각 집단에서 요소들에게 일련번호를 부여하여 추출하는 경우에 사용됩니다.
- 일부 집단을 랜덤하게 선택하고, 선택된 각 집단에서 표본을 무작위로 선택합니다.
- 모집단을 여러 군집으로 나누고, 그 중 몇 개의 군집을 무작위로 선택하여 그 안의 모든 구성원을 조사하는 방법입니다.
- 분할한 개개의 집단이 자체적으로 모집단을 잘 반영할 수 이도록 골고루 섞여있어야한다.
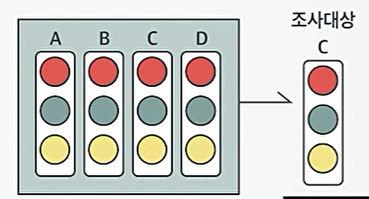
4. 층화추출법 (Stratified Sampling)
- 상대적으로 이질적인 요소들로 구성된 모집단에서 각종을 고루 대표할 수 있는 요소로 표본을 추출하는 방법입니다.
- 이질적인 모집단의 요소들을 서로 유사한 그룹(층)으로 나누고, 각 층에서 표본을 적절하게 추출합니다.
- 집단을 비슷한 특성을 가진 여러 층으로 나누고, 각 층에서 랜덤하게 표본을 추출합니다. 이 방법은 모집단 내의 다양성을 보다 잘 반영할 수 있습니다
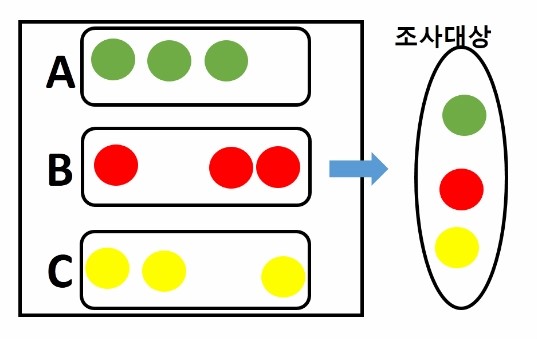
올바른 표본추출 방법을 선택하고 적용하는 것은 표본이 모집단을 대표할 수 있게 하여, 통계적 추론의 신뢰도를 높이는 데 매우 중요합니다.
'기초 통계' 카테고리의 다른 글
| No12.가설검증의 원리 (1) | 2024.04.22 |
|---|---|
| NO11_점추정과 구간추정 (1) | 2024.04.18 |
| No09_그래프에 의한 기술통계 (0) | 2024.04.16 |
| No08_수치적 기술통계 - 연관성 (1) | 2024.04.14 |
| No07_수치적 기술통계 - 변동성 (1) | 2024.04.13 |



