A. 확률변수의 개념
확률변수는 확률적인 실험의 결과에 수치를 할당하는 변수입니다.(표본공간에성 정의된 실수 값 함수)
이는 실험의 결과를 실수집합에 매핑하는 함수로, 각 결과에 대한 확률을 제공합니다. 확률변수는 대개 대문자로 표기되며, 예를 들어 X, Y와 같은 형태를 취합니다.
B. 확률분포함수
확률분포함수는 확률변수의 각 결과값에 대한 확률을 설명합니다. 이 함수는 확률변수가 특정 값 이하가 될 확률을 나타내는 누적분포함수(CDF)와 확률변수가 특정 값을 취할 확률을 나타내는 확률질량함수(PMF) 또는 확률밀도함수(PDF)로 구분됩니다.
- 이산 확률변수 : 확률질량함수가 사용되며, 특정 값을 취할 확률을 직접 나타냅니다./확률변수가 취할 수 있는 값이 셀 수 있는 경우
- ex) 고객, 사고 건수, 불량 수
- 예:
P(X=x) - 연속 확률변수 : 확률밀도함수가 사용되며, 확률변수의 값이 주어진 구간에서 모든 실수 값을 취할 수 있어 셀 수 없는 경우
- ex) 시간, 길이, 온도, 무게.
- 예:
P(a ≤ X ≤ b) = ∫_a^b f(x) dx
A. 확률변수의 개념
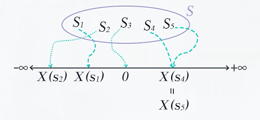
확률변수(Random Variable)는 확률실험의 각 결과에 실수 값을 할당하는 함수입니다. 이러한 할당을 통해 추상적인 실험 결과를 수치적인 분석의 대상으로 전환할 수 있습니다. 확률변수는 크게 두 가지 유형으로 나뉩니다: 이산 확률변수와 연속 확률변수입니다.
- 이산 확률변수(Discrete Random Variable): 셀 수 있는 값들을 취하며, 특정 값에 대한 확률을 직접 계산할 수 있습니다. 예를 들어, 동전 던지기의 결과나 주사위의 눈금 등이 이에 해당합니다.
- 연속 확률변수(Continuous Random Variable): 연속적인 값들을 취하며, 특정 구간에서 정의된 확률밀도함수를 통해 확률을 계산합니다. 예를 들어, 어떤 지점의 일일 온도나 측정된 높이 등이 이에 해당합니다.
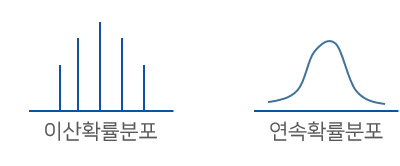
1. 확률질량함수(Probability Mass Function, PMF)
확률질량함수는 이산 확률변수의 각 가능한 값에 대한 확률을 제공합니다. PMF는 확률변수가 특정 값과 정확히 일치할 확률을 나타냅니다.
- 성질
- 모든 가능한 값에 대해 PMF의 합은 1입니다.
- 각 확률은 0 이상이어야 합니다.
- 이산 확률변수의 경우, 확률질량함수 \( f(x) \)는 특정 값 \( x \)를 취하는 확률을 나타냅니다.
- 식
PMF는 보통 다음과 같이 표기됩니다:
$$
f(x_i) = P(X = x_i) = p(x_i)
$$
여기서 \( p(x) \)는 확률변수 X가 \(x_i\) 값을 취할 확률을 나타냅니다.
2. 확률밀도함수(Probability Density Function, PDF)
확률밀도함수는 연속 확률변수에 대해 정의됩니다. PDF 자체는 확률을 직접 나타내지 않지만, 특정 구간에서의 적분을 통해 그 구간에 확률변수가 속할 확률을 계산할 수 있습니다.
- 성질
- PDF를 전 구간에 걸쳐 적분하면 그 값은 1입니다.
- PDF는 항상 0 이상의 값을 가집니다.
- 연속 확률변수의 경우, 확률밀도함수 ( f(x) )는 ( x )에서의 확률밀도를 나타내며, 구간 ( [a, b] )에 대한 확률은 ( f(x) )를 해당 구간에서 적분함으로써 구할 수 있습니다.
- 식
PDF는 일반적으로 다음과 같이 표기됩니다:
$$
P(a \leq X \leq b) = \int_{a}^{b} f(x) , dx
$$
또한 PDF는 다음 두 가지 성질을 만족합니다:
- \( f(x) \geq 0 ) for all ( x \)
- \( \int_{-\infty}^{\infty} f(x) , dx = 1 \)
3. 누적분포함수(Cumulative Distribution Function, CDF)
누적분포함수는 확률변수가 특정 값 이하일 확률을 나타내며, 이산 및 연속 확률변수 모두에 대해 정의됩니다. CDF는 확률변수의 모든 가능한 값에 대해 비감소하는 형태를 가집니다.
CDF는 모든 이산 및 연속 확률변수에 대해 정의되며, 확률변수의 분포를 완벽하게 설명합니다.
- 식
CDF는 다음과 같이 정의됩니다:
$$
F(x) = P(X \le x) = \int_{-\infty}^{x} f(t) , dt
$$
여기서 \( F(x) \)는 누적분포함수를, \( f(t) \)는 확률밀도함수를 의미합니다. 이산 확률변수의 경우, CDF는 확률질량함수의 누적합으로 계산됩니다.
C. 확률분포함수의 특성치
확률분포함수의 특성치는 분포의 중요한 수치적 특성을 나타내는 척도들입니다.
- 기대값(평균): 확률변수의 평균적인 값입니다. 이산 확률변수와 연속 확률변수 모두에 대해 계산할 수 있습니다.
E(X) = ∑ x P(X=x)또는E(X) = ∫ x f(x) dx- 분산: 확률변수의 값이 기대값에서 얼마나 퍼져있는지를 나타냅니다.
Var(X) = E[(X - E(X))^2]- 표준편차: 분산의 양의 제곱근으로, 확률변수의 퍼짐 정도를 나타내는 척도입니다.
σ(X) = √Var(X)
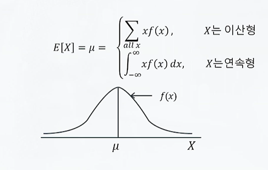
이러한 특성치는 확률분포의 형태와 확률변수의 값의 분포를 이해하는 데 핵심적인 요소입니다.
'기초 통계' 카테고리의 다른 글
| No07_수치적 기술통계 - 변동성 (1) | 2024.04.13 |
|---|---|
| NO.5 정규분포, 표준정규분포 (1) | 2024.04.02 |
| No4.이항분포, 포아송분포, 지수분포, 감마분포 (1) | 2024.03.28 |
| NO2.베이즈 정리 (0) | 2024.03.27 |
| No1. 확률의 개념과 특징 (0) | 2024.03.26 |



